Happy New Year....

Happy new year, wishing you all a very very happy 2010...

Let 2009 go away with all your sorrows and mistakes...

Dijkstra's Algorithm in C++

Dijkstra's Algorithm

Dijkstra's algorithm is a single source shortest path (sssp) algorithm. Like BFS, this famous graph searching algorithm is widely used in programming and problem solving, generally used to determine shortest tour in a weighted graph. This algorithm is almost similar to standard BFS, but instead of using a Queue data structure, it uses a heap like data structure or a priority queue to maintain the weight order of nodes. Here is the algorithm and pseudo-code. You can also look into Introduction to Algorithms (by C.L.R.S).

Here is a short implementation of this algorithm in C++, I assumed that, all the edge-weights are positive, and the max possible distance is less than 2²⁰ which is set as INF. The nodes are marked from 1 to N inclusive where N is the number of nodes.

Input format:

N E // number of nodes and edges
E lines containing an edge (u, v, w) on each line // edge(u, v, w) means weight of edge u-v is w. Nodes u, v are within range 1 to N
S // starting node

C++ code:

#include <cstdio>
#include <queue>
#include <vector>
using namespace std;

#define MAX 100001
#define INF (1<<20)
#define pii pair< int, int >
#define pb(x) push_back(x)

struct comp {
    bool operator() (const pii &a, const pii &b) {
        return a.second > b.second;
    }
};

priority_queue< pii, vector< pii >, comp > Q;
vector< pii > G[MAX];
int D[MAX];
bool F[MAX];

int main() {
    int i, u, v, w, sz, nodes, edges, starting;

    // create graph
    scanf("%d %d", &nodes, &edges);
    for(i=0; i<edges; i++) {
        scanf("%d %d %d", &u, &v, &w);
        G[u].pb(pii(v, w));
        G[v].pb(pii(u, w)); // for undirected
    }
    scanf("%d", &starting);

    // initialize distance vector
    for(i=1; i<=nodes; i++) D[i] = INF;
    D[starting] = 0;
    Q.push(pii(starting, 0));

    // dijkstra
    while(!Q.empty()) {
        u = Q.top().first;
        Q.pop();
        if(F[u]) continue;
        sz = G[u].size();
        for(i=0; i<sz; i++) {
            v = G[u][i].first;
            w = G[u][i].second;
            if(!F[v] && D[u]+w < D[v]) {
                D[v] = D[u] + w;
                Q.push(pii(v, D[v]));
            }
        }
        F[u] = 1; // done with u
    }

    // result
    for(i=1; i<=nodes; i++) printf("Node %d, min weight = %d\n", i, D[i]);
    return 0;
}

This is a straight forward implementation, according to the problem solving purpose, changes are to be made here and there.

Here is another implementation that does not use a custom comparison structure and the code is a bit more re-usable too. Note, that, nodes are numbered from 1 to n, pair for priority queue elements are assumed to be (weight, node) where pair for graph edges are assumed to be (node, weight). Also I have added comments to make the code more readable. Visit this codepad url for uncommented version of the code.

#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

typedef pair< int, int > pii;

/*
Set MAX according to the number of nodes in the graph. Remember,
nodes are numbered from 1 to N. Set INF according to what is the
maximum possible shortest path length going to be in the graph.
This value should match with the default values for d[] array.
*/
const int MAX = 1024;
const int INF = 0x3f3f3f3f;

/*
pair object for graph is assumed to be (node, weight). d[] array
holds the shortest path from the source. It contains INF if not
reachable from the source.
*/
vector< pii > G[MAX];
int d[MAX];

/*
The dijkstra routine. You can send a target node too along with
the start node.
*/
void dijkstra(int start) {
    int u, v, i, c, w;

    /*
    Instead of a custom comparator struct or class, we can use
    the default comparator class greater<T> defined in quque.h
    */
    priority_queue< pii, vector< pii >, greater< pii > > Q;

    /*
    Reset the distance array and set INF as initial value. The
    source node will have weight 0. We push (0, start) in the
    priority queue as well that denotes start node has 0 weight.
    */
    memset(d, 0x3f, sizeof d);
    Q.push(pii(0, start));
    d[start] = 0;

    /*
    As long as queue is not empty, check each adjacent node of u
    */
    while(!Q.empty()) {
        u = Q.top().second; // node
        c = Q.top().first; // node cost so far
        Q.pop(); // remove the top item.

        /*
        We have discarded the visit array as we do not need it.
        If d[u] has already a better value than the currently
        popped node from queue, discard the operation on this node.
        */
        if(d[u] < c) continue;

        /*
        In case you have a target node, check if u == target node.
        If yes you can early return d[u] at this point.
        */

        /*
        Traverse the adjacent nodes of u. Remember, for the graph,,
        the pair is assumed to be (node, weight). Can be done as
        you like of course.
        */
        for(i = 0; i < G[u].size(); i++) {
            v = G[u][i].first; // node
            w = G[u][i].second; // edge weight

            /*
            Relax only if it improves the already computed shortest
            path weight.
            */
            if(d[v] > d[u] + w) {
                d[v] = d[u] + w;
                Q.push(pii(d[v], v));
            }
        }
    }
}

int main() {
    int n, e, i, u, v, w, start;
    /*
    Read a graph with n nodes and e edges.
    */
    while(scanf("%d %d", &n, &e) == 2) {

        /*
        Reset the graph
        */
        for(i = 1; i <= n; i++) G[i].clear();

        /*
        Read all the edges. u to v with cost w
        */
        for(i = 0; i < e; i++) {
            scanf("%d %d %d", &u, &v, &w);
            G[u].push_back(pii(v, w));
            G[v].push_back(pii(u, w)); // only if bi-directional
        }

        /*
        For a start node call dijkstra.
        */
        scanf("%d", &start);

        dijkstra(start);

        /*
        Output the shortest paths from the start node.
        */
        printf("Shortest path from node %d:\n", start);
        for(i = 1; i <= n; i++) {
            if(i == start) continue;
            if(d[i] >= INF) printf("\t to node %d: unreachable\n", i);
            else printf("\t to node %d: %d\n", i, d[i]);
        }
    }
    return 0;
}

Dijkstra is a single source shortest path problem. So if you want to see the shortest path from every node, you have to call dijkstra once for each source or starting node.

Linked List in C

Linked List in C (covers insert, delete, sort, search, print)

Here it goes:

#include <stdio.h>
#include <stdlib.h>

typedef struct linked_list {
    int val;
    struct linked_list *next;
} LL;

LL *head, *tail;

void tail_insert(int v)
{
    if(head==NULL)
    {
        head = (LL *)malloc(sizeof(LL));
        head->val = v;
        head->next = NULL;
        tail = head;
    }
    else
    {
        LL *temp = (LL *)malloc(sizeof(LL));
        temp->val = v;
        temp->next = NULL;
        tail->next = temp;
        tail = tail->next;
    }
}

void head_insert(int v)
{
    if(head==NULL)
    {
        head = (LL *)malloc(sizeof(LL));
        head->val = v;
        head->next = NULL;
        tail = head;
    }
    else
    {
        LL *temp = (LL *)malloc(sizeof(LL));
        temp->val = v;
        temp->next = head;
        head = temp;
    }
}

void insert_before(int v, int n) // insert v before every n
{
    LL *curr, *temp;
    if(head!=NULL)
    {
        if(head->val==n)
        {
            temp = (LL *)malloc(sizeof(LL));
            temp->val = v;
            temp->next = head;
            head = temp;
            curr = head->next;
        }
        else curr = head;
        while(curr->next!=NULL)
        {
            if(curr->next->val==n)
            {
                temp = (LL *)malloc(sizeof(LL));
                temp->val = v;
                temp->next = curr->next;
                curr->next = temp;
                curr = curr->next;
            }
            curr = curr->next;
        }
    }
}

void insert_after(int v, int n) // insert v after every n
{
    LL *curr, *temp;
    if(head!=NULL)
    {
        curr = head;
        while(curr!=NULL)
        {
            if(curr->val==n)
            {
                temp = (LL *)malloc(sizeof(LL));
                temp->val = v;
                temp->next = curr->next;
                if(curr->next==NULL) tail = temp;
                curr->next = temp;
                curr = curr->next;
            }
            curr = curr->next;
        }
    }
}

void sort_linked_list()
{
    LL *i, *j, *k;
    int temp;
    k = tail;
    for(i=head; i!=tail; i=i->next)
    {
        for(j=head; ;j=j->next)
        {
            if(j->val > j->next->val)
            {
                temp = j->val;
                j->val = j->next->val;
                j->next->val = temp;
            }
            if(j->next==k)
            {
                k = j;
                break;
            }
        }
    }
}

void delete_all(int v) // deletes every v
{
    LL *temp, *curr = head;
    while(head!=NULL && head->val==v)
    {
        temp = head;
        head = head->next;
        free(temp);
        curr = head;
    }
    if(curr==NULL) return;
    while(curr->next!=NULL)
    {
        if(curr->next->val==v)
        {
            temp = curr->next;
            curr->next = curr->next->next;
            free(temp);
            if(curr->next==NULL) tail = curr;
        }
        else curr = curr->next;
    }
}

int search_linked_list(int v)
{
    LL *curr = head;
    int n = 0;
    while(curr!=NULL)
    {
        if(curr->val==v) return n;
        n++;
        curr = curr->next;
    }
    return -1;
}

void print_linked_list()
{
    LL *curr = head;
    while(curr!=NULL)
    {
        printf("%d ", curr->val);
        curr = curr->next;
    }
    printf("\n");
}

int main()
{
    int i, n, v;

    // insert at the end
    for(i=1; i<=5; i++)
        tail_insert(5);
    print_linked_list();

    // insert at the beginning
    for(i=1; i<=5; i++)
        head_insert(i);
    print_linked_list();

    for(i=1; i<5; i++)
    {
        scanf("%d %d", &n, &v);
        // insert v before every n
        insert_before(v, n);
        print_linked_list();
    }

    for(i=1; i<5; i++)
    {
        scanf("%d %d", &n, &v);
        // insert v after every n
        insert_after(v, n);
        print_linked_list();
    }

    // sort the list with bubble sort
    sort_linked_list();
    print_linked_list();

    for(i=0; i<5; i++)
    {
        scanf("%d", &v);
        // delete all v in the list
        delete_all(v);
        print_linked_list();
    }

    for(i=0; i<5; i++)
    {
        scanf("%d", &v);
        // see if there is v in the list
        n = search_linked_list(v);
        if(n==-1) printf("not found\n");
        else printf("found at %d\n", n);
    }
    return 0;
}

Everything is commented out, if more explanation needed, leave a comment...

Bitwise operations in C: Part 3

Bitwise Operation: Some applications

Back to Part 2

Binary number system is closely related with the powers of 2, and these special numbers always have some amazing bit-wise applications. Along with this, some general aspects will be briefly shown here.

Is a number a power of 2?
How can we check this? of course write a loop and check by repeated division of 2. But with a simple bit-wise operation, this can be done fairly easy.
We, know, the binary representation of p = 2ⁿ is a bit string which has only 1 on the n^th position (0 based indexing, right most bit is LSB). And p-1 is a binary number which has 1 on 0 to n-1 th position and all the rest more significant bits are 0. So, by AND-ing p and (p-1) will result 0 in this case:

p   = ....01000 &rArr 8
p-1 = ....00111 &rArr 7
-----------------------
AND = ....00000 &rArr 0

No other number will show this result, like AND-ing 6 and 5 will never be 0.

Swap two integers without using any third variable:
Well, as no 3^rd variable is allowed, we must find another way to preserve the values, how about we some how combine two values on one variable and the other will then be used as the temporary one...

Let A = 5 and B = 6
A = A ^ B = 3 /* 101 XOR 110 = 011 */
B = A ^ B = 5 /* 011 XOR 110 = 101 */
A = A ^ B = 6 /* 011 XOR 101 = 110 */
So, A = 6 and B = 5

Cool!!!

Divisibility by power of 2
Use of % operation is very slow, also the * and / operations. But in case of the second operand is a power of 2, we can take the advantage of bit-wise operations.
Here are some equivalent operations:

Here, P is in the form 2^X and N is any integer (typically unsigned)

N % P = N & (P-1)
N / P = N >> X
N * P = N << X

A lot faster and smarter...
About the % operation : the above is possible only when P is a power of 2

Masking operation
What is a mask? Its a way that is used to reshape something. In bit-wise operation, a masking operation means to reshape the bit pattern of some variable with the help of a bit-mask using some sort of bit-wise operation. Some examples following here (we won't talk about actual values here, rather we'll look through the binary representation and using only 16 bits for our ease of understanding):

Grab a portion of bit string from an integer variable.
Suppose A has some value like A = ... 0100 1101 1010 1001
We need the number that is formed by the bit-string of A from 3rd to 9th position.

[Lets assume, we have positions 0 to 15, and 0th position is the LSB]
Obviously the result is B = ... 01 1010 1; [we simply cut the 3rd to 9th position of A by hand]. But how to do this in programming.

Lets assume we have a mask X which contains necessary bit pattern that will help us to cut the desired portion. So, lets have a look how this has to be done:

A = 0100 1101 1010 1001
X = 0000 0011 1111 1000

See, we have X which have 1s in 3rd to 9th position and all the other thing is 0. We know, AND-ing any bit b with 1 leaves b unchanged.

So, X = X & A
Now, we have,
X = 0000 0001 1010 1000

So, now we've cut the desired portion, but this is exactly not what we wanted. We have 3 extra 0s in the tail, So just right-shift 3 times:

X = X >> 3 = 0000 0000 0011 0101; // hurrah we've got it.

Well, I got everything fine, but how to get such a weird X?

int x = 0, i, p=9-3+1; // p is the number of 1s we need
for(i=0; i<p, i++)
    x = (x << 1) | 1;
x = x << 3; // as we need to align its lsb with the 3rd bit of A

Execution:
X = 0000 0000 0000 0000 (initially X=0)
X = 0000 0000 0000 0001 (begin loop i=0)
X = 0000 0000 0000 0011 (i=1)
X = 0000 0000 0000 0111 (i=2)
X = 0000 0000 0000 1111 (i=3)
X = 0000 0000 0001 1111 (i=4)
X = 0000 0000 0011 1111 (i=5)
X = 0000 0000 0111 1111 (i=6 loop ends)
X = 0000 0011 1111 1000 (X=X<<3)

So, following the same approach, we may invert some portion of a bit-string (using XOR), make all bits 1 (using OR), make all bits in the portion 0 (using AND) etc etc very easily...

So, these are some tasks for the learner,
You have an integer A with some value, print the integers which have:
1. same bit pattern as A except it has all bits 0 within 4th to 23rd position.
2. same bit pattern as A except it has all bits 1 within 9th and 30th position.
3. same bit pattern as A except it has all bits inverted within positions 2nd and 20th.
4. totally inverted bit pattern.

Subset pattern:
Binary numbers can be used to represent subset ordering and all possible combination of taking n items.
For example, a problem might ask you to determine the n'th value of a series when sorted, where each term is some power of 5 or sum of some powers of 5.
It is clear that, each bit in a binary representation correspondence to a specific power of two in increasing order from right to left. And if we write down the consecutive binary values, we get some sorted integers. Like:

3 2 1 0 ⇒ power of 2
0 0 0 0 = 0 // took no one
0 0 0 1 = 1 // took power 0
0 0 1 0 = 2 // took power 1
0 0 1 1 = 3 // took power 1 and 0
0 1 0 0 = 4 // took power 2
0 1 0 1 = 5 // took power 2 and 0
0 1 1 0 = 6 // took power 2 and 1
0 1 1 1 = 7 // took power 2, 1 and 0
...........
...........
...........

So, what we do here is, take a power of 2 or take the sum of some powers of 2 to get a sorted sequence. Well, if this work for 2.. this will also work for 5 in the same way... Instead of taking the power of 2, we'll take the power of 5.
So the n'th term will be the sum of those powers of 5 on which position n's binary representation has 1. So the 10th term is 5³ + 5¹; As, 10₁₀ = 1010₂, it has 1 in 3rd and 1st position.

Worse than worthless
A bitwise GCD algorithm (wikipedia), translated into C from its assembly routine.

Sieve of Eratosthenes (SOE)
This is the idea of compressing the space for flag variables. For example, when we generate prime table using SOE, we normally use 1 int / bool for 1 flag, so if we need to store 10⁸ flags, we barely need 100MB of memory which is surely not available... and using such amount of memory will slow down the process. So instead of using 1 int for 1 flag, why don't we use 1 int for 32 flags on each of its 32 bits? This will reduce the memory by 1/32 which is less than 4MB :D

#define MAX 100000000
#define LMT 10000

unsigned flag[MAX>>6];

#define ifc(n) (flag[n>>6]&(1<<((n>>1)&31)))
#define isc(n) (flag[n>>6]|=(1<<((n>>1)&31)))

void sieve() {
    unsigned i, j, k;
    for(i=3; i<LMT; i+=2)
        if(!ifc(i))
            for(j=i*i, k=i<<1; j<MAX; j+=k)
                isc(j);
}

ifc(x) checks if x is a composite (if correspondent bit is 1)
isc(x) sets x as a composite (by making correspondent bit 1)

Other than this famous bit-wise sieve, we could use the technique in many places, to reduce memory for flagging.

Keep going on...

Bitwise operations in C: Part 2

Bitwise Operation: LEFT SHIFT and RIGHT SHIFT

Back to Part 1

<< (SHIFT LEFT) operator

This operator also depends highly on the length of the bit-string. Actually this operator only "shift" or moves all the bits to the left. This operator is mostly used if we want to multiply a number by 2, or, some powers of 2.
Example :

int a = 4978;
printf("%d\n", a<<1);

The output will be 9956. Do you see the relation between 4978 and 9956?

YES, 4978 * 2 = 9956. For more detailed explanation, we will see it in binary:

0001001101110010 ⇒ a = 4978(16 bit)
---------------- << 1 (SHIFT LEFT the bits by one bit)
0010011011100100 ⇒ 9956

Just move left all the bits by one. The left most bit is lost! and at the rightmost, a zero is added. Second example: count 4978 << 8 (count 4978 shifted left by 8 bits)
Answer:

0001001101110010 ⇒ 4978 (16 bit representation)
---------------- << 8 (SHIFT LEFT the bits by 8 bit)
0111001000000000 ⇒ 29184

So, using 16 bit compiler, 4978 << 8 is 29184, which is incorrect! Some of the left most bits are lost...It will not, however, if we use 32 bits data type.

00000000000000000001001101110010 ⇒ 4978(32 bit)
-------------------------------- << 8 (SHIFT LEFT the bits by 8 bit)
00000000000100110111001000000000 ⇒ 1274368

I've told you before that, this operator depends the length of bit-string. Don't be surprised if you got the output of 4978 << 8 is 1274368. (this is actually correct!) As we see, no bits are lost after shifting the bits left by 8 bits if we use a 32 bit data type.
Note that you don't have to have an int to store the value! In C, you can just print like this :

printf("%d", 4978 << 8);

The output will be 29184 for 16 bit compiler as Turbo C (16 bits; some bits will be lost)
The output will be 1274368 for 32 bit compiler as GNU C (32 bits; all bits are reserved since it has bigger capacity)
Now you know why shifting left 1 bit is the same as multiply the number by 2 right?
And shifting left 8 bits is exactly the same as multiplying the number by 2⁸.

4978 << 8 = 1274368 (in 32 bits compiler)
4978 * 2⁸ = 4978 * 256 = 1274368. (exactly the same)

BTW, we need to be careful when using signed data type, as the left most bit is the sign bit. So, while left shifting, if you push a 1 at that position, the number will be negative.

>> (SHIFT RIGHT) operator

Not much different with << (SHIFT LEFT) operator. It just shifts all the bits to the right instead of shifting to the left. This operator is mostly used if we want to divide a number by 2, or, some powers of 2.

Example :

count 4978 >> 8

int a = 4978;
printf("%d\n", a>>8);

4978 >> 8 = 19 (in 16 bits compiler or 32 bits compiler, the >> has no difference, because >> will discard the right most bit, and increased capacity on the left side doesn't help here anyhow)

Detailed explanation :

0001001101110010 ⇒ 4978(16 bit)
---------------- >> 8 (SHIFT RIGHT the bits by 8 bit)
0000000000010011 ⇒ 19

and

00000000000000000001001101110010 ⇒ 4978(32 bit)
-------------------------------- >> 8 (SHIFT RIGHT the bits by 8 bit)
00000000000000000000000000010011 ⇒ 19

If you notice:

4978 >> 8 = 19 (in 32 bits compiler)

4978 / 2⁸ = 4978 / 256 = 19. (They both the same, but using bit-wise operator >> (SHIFT RIGHT) is a LOT faster!)

The RIGHT SHIFT operator is machine dependent, it may work differently on different machines for signed data types. >> empties the left most bit and that is filled either by a 0 or by a 1, depending on the machine.
Filled by a 1 (RIGHT SHIFT ARITHMETIC)
Filled by a 0 (RIGHT SHIFT LOGICAL)
Example:

signed char x = -75 /* 1011 0101 */
signed char y = x >> 2

/* result of logical right shift */
y = 45  /* 0010 1101 */

/* result of arithmetic right shift */
y = -19 /* 1110 1101 */

So this behavior of RIGHT SHIFT leads to a non-portability of a program.

A few more words

The two shift operators are generally used with unsigned data type to avoid ambiguity.
Result of Shifting Right or Left by a value which is larger than the size of the variable is undefined.
Result of shifting Right or Left by a negative value is also undefined.

Order precedence of the basic operators is:

NOT ( ~ ) highest
AND ( & )
XOR ( ^ )
 OR ( | ) lowest

Some basic operations:

Let X is a single bit, then we can write the following: 
X & 1 =  X; X & 0 =  0
X | 1 =  1; X | 0 =  X
X ^ 1 = ~X; X ^ 0 =  X

Bit-wise operations are quite fast and easy to use, sometimes they reduce the running time of your program heavily, so use bit-wise operations when-ever you can. But if you look on the software developing aspect, they are not much reliable because, they aren't applicable with any type of data, especially floating points, and signed types. Also, not many people understand them.

But, still, who cares? I want to give some scary looks to my code... lol :D
Hopefully, on the next post, we'll see some simple ideas which will implement some bit-wise operations...

Continue to Part 3

Bitwise operations in C: Part 1

Bitwise Operation: AND, OR, XOR, NOT

In computer, all the numbers and all the other data are stored using 2 based number system or in binary format. So, what we use to say a '5' in decimal (do we use decimal only because we have 10 figures? who knows...), a computer will represent it as '101', in fact, everything is represented as some sequence of 0s and 1s. We call this sequence a bit-string.

Bit-wise operations means working with the individual bits other than using the larger or default data types, like integers, floating points, characters, or some other complex types. C/C++ provides a programmer an efficient way to manipulate individual bits of a data with the help of commonly known logical operators like AND(&), OR(|), NOT(~), XOR(^), LEFT SHIFT(<<) and RIGHT SHIFT(>>) operators.

To be fluent with bit-wise operations, one needs to have a clear concepts about how data is stored in computer and what is a binary number system.

From a programming contest aspect, we'll explore bit-wise operations for only integer types (int in C/C++) and as this is almost 2010, we'll consider int as a 32 bit data type. But for the ease of writing, sometimes only the lowest 16 bits will be shown. The above operators works on bit-by-bit, i.e. during bit-wise operation, we have to align right the bits! (just like addition, multiplication,...) The shorter bits always have leading 0s at the front. And another important thing... we do not need to convert the integers to the binary form ourselves, when we use the operators, they will be automatically evaluated and the following examples shows the underlying activities... :P

& (AND) operator

This table will clearly explains the bit-wise operator & (AND):

0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1

Example:
What is the value of 24052 & 4978 ?
To solve this, we have to consider the operations in base 2.
So, we imagine both numbers in base 2 and align right the bits, as shown below using 16 bits. Now, AND the numbers : (shorter bits can have leading zeros at the front):

101110111110100 ⇒ 24052
001001101110010 ⇒ 4978
--------------- &
001000101110000 ⇒ 4464

Each bit-column is AND-ed using the AND table above.

| (OR) operator

This table summarizes the OR operations :

0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1

Now, using the same example above, let's do it using | (OR) operator :

101110111110100 ⇒ 24052
001001101110010 ⇒ 4978
--------------- |
101111111110110 ⇒ 24566

Each bit-column is OR-ed using the OR table above.

^ (XOR) operator

This table summarize the XOR operations :

0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0

Now, using the same example above, let's do using ^ (XOR) operator :

101110111110100 ⇒ 24052
001001101110010 ⇒ 4978
--------------- ^
100111010000110 ⇒ 20102

Easy, isn't it?

~ (NOT) operator

This operator is different from the above operators. This operator is called unary operator, since it only needs one operand. The operators &, |, ^ are binary operators, since it takes 2 operands/number to be operated.

This ~ (NOT) operator, inverts all the bits in a variable. That is, changes all zeros into ones, and changes all ones into zeros.
Remember! that the result of this ~ (NOT) operation highly depends on the length of the bit-string.

Example:

int a = 10;
printf("%d\n", ~a);

Surprisingly, the output is -11. But actually this is normal as most of the cases computer represents negative numbers in the 2's complement form. Look at the operation shown below using 16 bits:

0000000000001010 ⇒ a(16 bits)
---------------- ~
1111111111110101 ⇒ -11

This is correct! Because computer stores -11 as 1111111111110101 in binary! (in the 2's complement form). Even if we use 32 bits representation, it is still the 2's complement form of -11;

-11(10) = 11111111111111111111111111110101(2)

Anyway, if we do the same operation for unsigned int:

unsigned int a = 10;
printf("%u\n", ~a);

Hah ha, don't be surprised if you get the output of the unsigned value of -11 is 4294967285.

If you use 32 bits, you actually will get -11 as 11111111111111111111111111110101 in signed binary representation:

00000000000000000000000000001010 ⇒ 10 (32 bits)
-------------------------------- ~
11111111111111111111111111110101 ⇒ -11 (for signed) and -> 4294967285 (for unsigned)

In the unsigned data type, all the bits are considered to be the part of the magnitude, there's no bit position reserved for sign bits.

Continue to Part 2

Power Series Evaluation

Power series evaluation in O(lg(n)):[n is the number of terms]

We'll try to evaluate the following power series in logarithmic time w.r.t. the number of terms n.


Well well... I may be asked, "dude, why do you want to do this in O(lg(n)) when there's already we have a O(1) solution for your problem?". Answer is simple, "I'm trying it from a programming perspective and the O(1) can get sometimes impossible when n keeps going up i.e. like 10¹⁰⁰⁰ and you are asked to return the answer w.r.t. some %m [modulus m] (meaning the final result will not reach m). This method will be suitable for this case only. Because, calculating {(x^n-1-1)/(x-1)}%m is not a very easy task and sometimes, it is not directly possible.

This series can be evaluated by binary splitting and recursively solving those building up the answer.
Let n = 6
We have, 1 + x + x² + x³ + x⁴ + x⁵
⇒ (1 + x + x²) + x³(1 + x + x²)
⇒ (1 + x + x²)(1 + x³)

So, when n is even, f(x, n) = (1 + x^n/2)f(x, n/2)

Now, what if n is odd, Let n = 7
We have, 1 + x + x² + x³ + x⁴ + x⁵ + x⁶
⇒ (1 + x + x²) + x³(1 + x + x²) + x⁶
⇒ (1 + x + x²)(1 + x³) + x⁶

So, when n is odd, f(x, n) = (1 + x^n/2)f(x, n/2) + x^n-1

So, by combining the above 2 equations, we get the final solution:
f(x, n) = (1 + x^n/2)f(x, n/2) + (n%2)x^n-1

By some clever observation, the need for -1 and %2 operation on n can be eliminated. So, the only thing we need to do is the /2 operation on n, which is easy even when n is a big integer.

Here is a python module that shows only the recursive part, no trick applied.

import math

def evaluate(x, n):
    if(n==0):
        return 0
    if(n==1):
        return 1
    ret = 0
    if(n%2==1):
        ret = ret + int(math.pow(x, n-1))
    n = n/2
    return ret + evaluate(x, n)*(1 + int(math.pow(x, n)))

If this is to be done with C/C++, some biginteger division algorithm should be implemented.

Easy, eh? Check different types of series here

Gauss–Jordan Elimination

Gauss–Jordan Elimination in C++

This is my first attempt to solve linear systems with unique solutions in O(N³).

Algorithm:
1. Read augmented matrix for the system.
2. Perform Gaussian Elimination to get the matrix in row echelon form.
3. Transform the matrix to reduced row echelon form.
4. Write results.

Preview:

[click for a clear view]

My C++ solution (change MAX to desired size, it is the maximum limit of how many equations it can handle, change the macro DEBUG to "if(1)" if you want to see the intermediate steps):

#include <iostream>
#include <cstdlib>
#include <cassert>
#include <algorithm>
using namespace std;

#define DEBUG if(0)
#define MAX 5

struct MAT {
    int R[MAX+1];
} M[MAX];

int N;

int gcd(int a, int b) {
    while(b) b ^= a ^= b ^= a %= b;
    return a;
}

bool comp(MAT A, MAT B) {
    for(int k=0; k<N; k++) {
        if(A.R[k] > B.R[k]) return true;
        if(A.R[k] < B.R[k]) return false;
    }
    return true;
}

void print(void) {
    int i, j;
    cout << "..." << endl;
    for(i=0; i<N; i++) {
        for(j=0; j<N; j++) cout << M[i].R[j] << '\t';
        cout << M[i].R[j] << endl;
    }
    cout << "..." << endl;
}

void modify(MAT &A, MAT B, int a, int b) {
    for(int r=0; r<=N; r++) A.R[r] = a*B.R[r] - b*A.R[r];
}

void eliminate(void) {
    int i, g, k;
    for(i=0; i<N-1; i++) {
        if(!M[i].R[i]) {
            sort(&M[i], M+N, comp);
            assert(M[i].R[i]);
        }
        for(k=i+1; k<N; k++) {
            g = gcd(abs(M[i].R[i]), abs(M[k].R[i]));
            modify(M[k], M[i], M[k].R[i]/g, M[i].R[i]/g);
        }
        DEBUG print();
    }
}

void reduce(void) {
    int i, g, k;
    for(i=N-1; i; i--) {
        for(k=i-1; k>=0; k--) {
            g = gcd(abs(M[i].R[i]), abs(M[k].R[i]));
            modify(M[k], M[i], M[k].R[i]/g, M[i].R[i]/g);
        }
        DEBUG print();
    }
}

void printsol(void) {
    double h, l;
    cout << "Solve for " << N << " variables:" << endl;
    for(int i=0; i<N; i++) {
        assert(M[i].R[i]);
        h = M[i].R[i];
        l = M[i].R[N];
        cout << 'x' << i+1 << " = " << l/h << endl;
    }
    cout << "..." << endl;
}

int main(void) {
    int i, j, g;
    while(cin >> N) {
        if(!N) break;
        memset(M, 0, sizeof(M));
        for(i=0; i<N; i++) {
            for(j=0; j<N; j++) cin >> M[i].R[j];
            cin >> M[i].R[j];
            for(j=g=0; j<=N; j++) g = gcd(abs(M[i].R[j]), g);
            for(j=0; j<=N; j++) M[i].R[j] /= g;
        }
        eliminate();
        reduce();
        printsol();
    }
    return 0;
}

However, I'm trying to do it in a more efficient way. I'll post that when I'm done.

Attacking Recursions

Some general approach for solving recursive problems:

If anyone want to read an awesome super cool tutorial on recursion in BANGLA... read from Fahim Vai's page

#1: Forget about what you need to do, just think about any input, for which you know what your function should output, as you know this step, you can build up a solution for your problem. Suppose you have a function which solves a task, and you know, this task is somehow related to another similar task. So you just keep calling that function again and again thinking that, the function I'm calling will solve the problem anyhow, and the function will also say, I'll solve this problem, if you give me the result for another sub-problem first!!! Well, then you'll say, "So, why don't you use your twin-brother to solve that part?" and so on... The following example will show you how to start writing a recursive function.

Example: Think about computing n! recursively. I still don't know what and how my function will do this. And I also don't know, like what could be 5! or 7!... But nothing to worry about, I know that 0! = 1! = 1. And I also know that, n! = n(n-1)!. So I will think like that, "I will get n! from a function F, if some one gives me (n-1)!, then I'll multiply it with n and produce results". And, thus, F is the function for computing n!, so why don't I use again to get (n-1)! ? And when F tries to find out what could be the value of (n-1)!, it also stumbles at the same point, it wonders what would be the value of (n-2)!... then we tell him to use F again to get this... and this thing keeps going as long as we don't know what F actually should return for any k. In case of k = 1, as we know now F can return 1 for k = 1, and it don't need to call another F to solve anything first...

int factorial(int n) {
    // I know this, so I don't want my function to go any further...
    if(n==0) return 1;
    // don't bother what to do, just reuse the function...
    else return n*factorial(n-1);
}

#2: What ever you can do with loops, can be done with recursions as well. A simple technique for converting recursions and loops is shown below:

Forward:
for loop:

for(int i = 0; i < n; i++) {
    // do whatever needed
}

Equivalent recursion:

void FOR(int i, int n) {
    if(i==n) return; // terminates
    // do whatever needed
    FOR(i+1, n); // go to next step
}

Backward:
for loop:

for(int i = n-1; i >= 0; i -= 1) {
    // do whatever needed
}

Equivalent recursion:

void ROF(int i, int n) {
    if(i==n) return; // terminates
    ROF(i+1, n); // keep going to the last
    // do whatever needed when returning from prev steps
}

Well, you may wonder how this is backward loop? But just think of its execution cycle, just after entering the function, it is calling itself again incrementing the value of i, and the execution routine that you have written under the function call, was paused there. From the new function it enters, it works the same way, call itself again before executing anything...Thus when you have reached the limiting condition, or the base condition, then the function stops recursion and starts returning, and the whole process can be shown as below...let n=5, and we want to print 5 4 3 2 1...code for this might be:

void function(int i, int n) {
    if(i<=n) {
        function(i+1, n);
        printf("%d ", i);
    }
}

Explanation might look like this:

01|call function1 with i=1
02|    call function2 with i=2
03|        call function3 with i=3
04|            call function4 with i=4
05|                call function5 with i=5
06|                    call function6 with i=6
07|                        i breaks condition, no more calls
08|                    return to function5
09|                    print 5
10|                return to function4
11|                print 4
12|            return to function3
13|            print 3
14|        return to function2
15|        print 2
16|    return to function1
17|    print 1
18|return to main, done!

Left side number shows the execution steps, so from the above program, we get, 5 4 3 2 1. So indeed it ran on reverse direction...

#3: Use the advantage of call stack. When you call functions recursively, it stays in the memory as the following picture demonstrates.

int f(int n) {
    if(n==0) return 1;
    return n*f(n-1);
}

You know about stack, in a stack, you cannot remove any item unless it is the topmost. So you can consider the calling of a recursive function as a stack, where, you can't remove the memory used by f(n=3) before removing f(n=2) and so so... So, you can easily see that, the functions will hold all their variables and values until it is released. This actually serves the purpose of using an array.

#4: Be careful while using recursions. From a programming contest aspects, recursions are always best to avoid. As you've seen above, most recursions can be done using loops somehow. Recursions have a great deal of drawbacks and it most of the time extends the execution time of your program. Though recursions are very very easy to understand and they are like the first idea in many problems that pops out in mind first... they still bear the risks of exceeding memory and time limits.



Generally, in loops, all the variables are loaded at the same time which causes it a very low memory consumption and faster access to the instructions. But whenever we use recursions, each function is allotted a space at the moment it is called which requires much more time and all the internal piece of codes stored again which keeps the memory consumption rising up. As your compiler allows you a specific amount of memory (generally 32 MB) to use, you may overrun the stack limit by excessive recursive calls which causes a Stack Overflow error (a Runtime Error).



So, please think a while before writing recursions whether your program is capable of running under the imposed time and memory constraints. Generally recursions in O(lg n) are safe to use, also we may go to a O(n) recursion if n is pretty small.

#5: If the recursion tree has some overlapping branches, most of the times, what we do, is to store already computed values, so, when we meet any function which was called before, we may stop branching again and use previously computed values, which is a common technique knows as Dynamic Programming (DP), we will talk about that later as that is pretty advanced.

These techniques will be used in almost all problems when writing recursive solution. Just don't forget the definition of recursion:
Definition of recursion = See the Definition of recursion

Now try this

Drawing Regular n-gon

How to draw a regular pentagon with just ruler and compass?

How about a regular hexagon?

Underlying theorem:
Primes of the form 2²ⁿ + 1 are known as Fermat primes.

A regular n-gon is constructible using straightedge (ruler) and compass if and only if n = 2ⁱ · m where m is a product of any number of distinct Fermat Prime and i is any natural number, including zero.


Only five Fermat primes are known: 3, 5, 17, 257, and 65,537.

Related study: Compass and straightedge constructions.

Practice Recursions

Recursions are fun

You may like to try out some simple problems to practice recursions. Try to solve all of them without using any global variables. And try on your own before looking at the solutions. Also please notify any error to me ( zobayer1[at]gmail[dot]com ). Before looking at the problems, you may like to read this post about how to attack recursive problems.

Problem 1:

You will be given an array of integers, write a recursive solution to print it in reverse order.

Input:
5
69 87 45 21 47
Output:
47 21 45 87 69

see answer

Problem 2:

Write a recursive function to print an array in the following order. [0] [n-1] [1] [n-2] ......... ......... [(n-1)/2] [n/2]

Input:
5
1 5 7 8 9
Output:
1 9
5 8
7 7

see answer

Problem 3:

Write a recursive program to remove all odd integers from an array. You must not use any extra array or print anything in the function. Just read input, call the recursive function, then print the array in main().

Input:
6
1 54 88 6 55 7
Output:
54 88 6

see answer

Problem 4:

Write a recursive solution to print the polynomial series for any input n: 1 + x + x² + ................. + x^n-1

Input:
5
Output:
1 + x + x^2 + x^3 + x^4

see answer

Problem 5:

Write a recursive solution to evaluate the previous polynomial for any given x and n. Like, when x=2 and n=5, we have 1 + x + x² + ................. + x^n-1 = 31

Input:
2 5
Output:
31

see answer

Problem 6:

Write a recursive program to compute n!

Input:
5
Output:
120

see answer

Problem 7:

Write a recursive program to compute n^th fibonacci number. 1^st and 2^nd fibonacci numbers are 1, 1.

Input:
6
Output:
8

see answer

Problem 8:

Write a recursive program to determine whether a given integer is prime or not.

Input:
49
999983
1
Output:
not prime
prime
not prime

see answer

Problem 9:

Write a recursive function that finds the gcd of two non-negative integers.

Input:
25 8895
Output:
5

see answer

Problem 10:

Write a recursive solution to compute lcm of two integers. You must not use the formula lcm(a,b) = (a x b) / gcd(a,b); find lcm from scratch...

Input:
23 488
Output:
11224

see answer

Problem 11:

Suppose you are given an array of integers in an arbitrary order. Write a recursive solution to find the maximum element from the array.

Input:
5
7 4 9 6 2
Output:
9

see answer

Problem 12:

Write a recursive solution to find the second maximum number from a given set of integers.

Input:
5
5 8 7 9 3
Output:
8

see answer

Problem 13:

Implement linear search recursively, i.e. given an array of integers, find a specific value from it. Input format: first n, the number of elements. Then n integers. Then, q, number of query, then q integers. Output format: for each of the q integers, print its index (within 0 to n-1) in the array or print 'not found', whichever is appropriate.

Input:
5
2 9 4 7 6
2
5 9
Output:
not found
1

see answer

Problem 14:

Implement binary search recursively, i.e. given an array of sorted integers, find a query integer from it. Input format: first n, the number of elements. Then n integers. Then, q, number of query, then q integers. Output format: for each of the q integers, print its index (within 0 to n-1) in the array or print 'not found', whichever is appropriate.

Input:
5
1 2 3 4 5
2
3 -5
Output:
2
not found

see answer

Problem 15:

Write a recursive solution to get the reverse of a given integer. Function must return an int

Input:
123405
Output:
504321

see answer

Problem 16:

Read a string from keyboard and print it in reversed order. You must not use any array to store the characters. Write a recursive solutions to solve this problem.

Input:
helloo
Output:
oolleh

see answer

Problem 17:

Write a recursive program that determines whether a given sentence is palindromic or not just considering the alpha-numeric characters ('a'-'z'), ('A'-'Z'), ('0'-'9').

Input:
madam, i'm adam
hulala
Output:
palindromic
not palindromic

see answer

Problem 18:

Implement strcat(), stracpy(), strcmp() and strlen() recursively.

Input:
test on your own
Output:
test on your own

see answer

Problem 19:

If you already solved the problem for finding the n^th fibonacci number, then you must have a clear vision on how the program flow works. So now, in this problem, print the values of your fibonacci function in pre-order, in-order and post-order traversal. For example, when n = 5, your program calls 3 and 4 from it, from the call of 3, your program calls 1 and 2 again....... here is the picture:

Input:
5
Output:
Inorder: 1 3 2 5 2 4 1 3 2
Preorder: 5 3 1 2 4 2 3 1 2
Postorder: 1 2 3 2 1 2 3 4 5

see answer

Problem 20:

All of you have seen the tower of Hanoi. You have 3 pillars 'a', 'b' and 'c', and you need transfer all disks from one pillar to another. Conditions are, only one disk at a time is movable, and you can never place a larger disk over a smaller one. Write a recursive solution to print the moves that simulates the task, a -> b means move the topmost of tower a to tower b.

Input:
3
Output:
a -> c
a -> b
c -> b
a -> c
b -> a
b -> c
a -> c

see answer

Good Luck!!!

Volume of an irregular tetrahedron

Find the volume of an irregular tetrahedron form its edges:

Suppose you are given the 6 sides of an irregular tetrahedron and you need to find the volume consumed by it.

Let the given sides to be u, v, w, W, V, U. Here, (u, U), (v, V), (w, W) are considered to be opposite edge pairs ( opposite edges means the edges which do not share common vertices ). Now the volume can be found from the following formula:

Let:
u′ = v² + w² - U²
v′ = w² + u² - V²
w′ = u² + v² - W²
Now:
volume = ¹⁄₁₂ × √(4u²v²w² - u²u′² - v²v′² - w²w′² + u′v′w′)

This formula is derived from the determinant which can be found here for more reading. As the formula is symmetric, the ordering of the pairs won't make any change to the formula.

Read more properties about Tetrahedrons from Wikipedia.

Contest Template

C++ contest coding template. Edit:5.

/*
USER: zobayer
TASK: template
ALGO: template
*/
#include <cassert>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <iostream>
#include <sstream>
#include <iomanip>
#include <string>
#include <vector>
#include <list>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <algorithm>
#include <iterator>
#include <utility>
using namespace std;

template< class T > T _abs(T n) { return (n < 0 ? -n : n); }
template< class T > T _max(T a, T b) { return (!(a < b) ? a : b); }
template< class T > T _min(T a, T b) { return (a < b ? a : b); }
template< class T > T sq(T x) { return x * x; }
template< class T > T gcd(T a, T b) { return (b != 0 ? gcd<T>(b, a%b) : a); }
template< class T > T lcm(T a, T b) { return (a / gcd<T>(a, b) * b); }
template< class T > bool inside(T a, T b, T c) { return a<=b && b<=c; }
template< class T > void setmax(T &a, T b) { if(a < b) a = b; }
template< class T > void setmin(T &a, T b) { if(b < a) a = b; }

#define MP(x, y) make_pair(x, y)
#define REV(s, e) reverse(s, e)
#define SET(p) memset(p, -1, sizeof(p))
#define CLR(p) memset(p, 0, sizeof(p))
#define MEM(p, v) memset(p, v, sizeof(p))
#define CPY(d, s) memcpy(d, s, sizeof(s))
#define READ(f) freopen(f, "r", stdin)
#define WRITE(f) freopen(f, "w", stdout)
#define ALL(c) c.begin(), c.end()
#define SIZE(c) (int)c.size()
#define PB(x) push_back(x)
#define ff first
#define ss second
#define i64 __int64
#define ld long double
#define pii pair< int, int >
#define psi pair< string, int >

const double EPS = 1e-9;
const double BIG = 1e19;
const int INF = 0x7f7f7f7f;

int main() {
    //READ("in.txt");
    //WRITE("out.txt");
    return 0;
}

Segment-Circle Intersection

This is a sample code which verifies whether a given Circle and Segment intersects or not.

/*
**  Verifies the intersection of a segment and a circle
**  The line segment is defined from points p1 to p2
**  The circle is of radius r and centered at point c
**  There are potentially two points of intersection given by
**  p = p1 + mu1 (p2 - p1)
**  p = p1 + mu2 (p2 - p1)
**  mu1 and mu2 are updated via reference
**  Return FALSE if the segment doesn't intersect the circle
*/
bool cross(POINT p1, POINT p2, CIRCLE p, double &mu1, double &mu2) {
    double a, b, c, d;
    POINT t;
    t.x = p2.x - p1.x;
    t.y = p2.y - p1.y;
    a = sq(t.x) + sq(t.y);
    b = 2.0 * (t.x * (p1.x - p.c.x) + t.y * (p1.y - p.c.y));
    c = sq(p.c.x) + sq(p.c.y);
    c += sq(p1.x) + sq(p1.y);
    c -= 2.0 * (p.c.x * p1.x + p.c.y * p1.y);
    c -= sq(p.r);
    d = b * b - 4 * a * c;
    if(fabs(a) < eps || d < -eps) {
        mu1 = mu2 = 0.0;
        return false;
    }
    mu1 = (-b + sqrt(d)) / (2.0 * a);
    mu2 = (-b - sqrt(d)) / (2.0 * a);
    return true;
}

SPOJ Hints

Thanks to the Japanese boy, from whom I got this list. But unfortunately I could not read his name.. (Sorry! I can't read Japanese language.)

I've edited the list and added some myself (uploaded on Google Docs). This list is going to updated time by time...

Here is the file, have a look.
[Last updated: Thursday, November 12, 2009]

If any mistake is found, please comment out here. Thanks...

Linux : Bash Script (Shell Script)

A very simple automatic judge:

All of you studying cse must have known what is an Onlinejudge and most of us don't know how it works. Btw, I'm not going to talk about that here. It's a simple Linux Shell Scripting example / tutorial which will show you how to handle other programs in Bash and how to access all the files in a specific folder not knowing exactly how many are there.

The following snippet works very simply. It takes a target [.cpp] file as a command line argument and compiles it using g++, generates output files for all the input files provided with. And last, it compares those files with original output files and checks whether your program generated all the outputs correctly. So you can use it for your own purposes by making proper modification. It's also very easy to understand.

Note:
The folder from where you run this script must have these in it:
1. in // it will contain the input files with [.in] extension.
2. pout // it will hold the output files generated by your program.
3. jout // it will contain the correct judge output files for testing.
4. The program you are checking for with obviously [.cpp] extension and it's name is to be passed by command line argument.
Unless you change them in the code as you like. It is always a good practice to experiment with codes. :)

# Author: Zobayer Hasan
# CSE DU - 22/10/2009

# Check whether target file is provided or exists
# If available, compile and make it executableclear

if [ $# != 1 ]; then
    echo "parameter missing"
    exit
elif [ ! -f "$1" ]; then
    echo "file not found"
    exit
else
    if [ -f PROG ]; then
        rm PROG
    fi

    g++ -o PROG "$1"

    if [ ! -f PROG ]; then
        echo "Compilation Error!"
        echo "Your program could not be compiled."
        echo ;
        exit
    fi

    chmod -c 777 PROG > log.txt
fi

# Run the executable for each file in the "in" directory
# And generate their output files in "pout" directory
# Then match with the correct files in "jout" directory

echo ;

N=0
values=$( ls ./in/*.in )

for LINE in $values
do
    ./PROG < "$LINE" > "./pout/$N.out"
    diff ./pout/$N.out ./jout/$N.out > log.txt

    if [ $? -eq 1 ]; then
        echo "Wrong Answer!"
        echo "For file $LINE. Check log file."
        echo ;
        exit
    fi

    N=$(( N + 1 ))
done

echo "Accepted!"
echo "All tests passed successfully."
echo ;

# End of script :)

Have fun with bash !!!

SPOJ Solve list comparison tool

Check this:

This is a tool for comparing solve list between two users in SPOJ... Of-course you can do that with your eyes, but that's no doubt tedious...

http://www.cise.ufl.edu/~mlpalii/spoj/head2head.pl?user1=<user_id_1>&user2=<user_id_2>

This is the address of the tool.... You just need to replace the <user_id_1> and <user_id_2> with your desired two spoj user ID.

Example: say, two users "zobayer" and "shiplu", their head2head comparison is here:
http://www.cise.ufl.edu/~mlpalii/spoj/head2head.pl?user1=zobayer&user2=shiplu

Also, this site is great :: https://www.otinn.com/spoj/comparer.php (thanks to Ridowan)

Segmented Sieve

Memory and time efficient :)

Problem Statement:

Your are given two integers a and b. You have to find all the primes within range a and b. Here, 1 ≤ a ≤ b ≤ 2³¹-1 and b - a ≤ 10⁵.

Note: You have to handle 1, 2 and even numbers for appropriate case of your own.

Solution:

#include <string.h>

#define MAX 46656
#define LMT 216
#define LEN 4830
#define RNG 100032

unsigned base[MAX/64], segment[RNG/64], primes[LEN];

#define sq(x) ((x)*(x))
#define mset(x,v) memset(x,v,sizeof(x))
#define chkC(x,n) (x[n>>6]&(1<<((n>>1)&31)))
#define setC(x,n) (x[n>>6]|=(1<<((n>>1)&31)))

/* Generates all the necessary prime numbers and marks them in base[]*/
void sieve()
{
    unsigned i, j, k;
    for(i=3; i<LMT; i+=2)
        if(!chkC(base, i))
            for(j=i*i, k=i<<1; j<MAX; j+=k)
                setC(base, j);
    for(i=3, j=0; i<MAX; i+=2)
        if(!chkC(base, i))
            primes[j++] = i;
}

/* Returns the prime-count within range [a,b] and marks them in segment[] */
int segmented_sieve(int a, int b)
{
    unsigned i, j, k, cnt = (a<=2 && 2<=b)? 1 : 0;
    if(b<2) return 0;
    if(a<3) a = 3;
    if(a%2==0) a++;
    mset(segment,0);
    for(i=0; sq(primes[i])<=b; i++)
    {
        j = primes[i] * ( (a+primes[i]-1) / primes[i] );
        if(j%2==0) j += primes[i];
        for(k=primes[i]<<1; j<=b; j+=k)
            if(j!=primes[i])
                setC(segment, (j-a));
    }
    for(i=0; i<=b-a; i+=2)
        if(!chkC(segment, i))
            cnt++;
    return cnt;
}

This is a sample program which demonstrates segmented sieve. Very fast and memory efficient version. 'base' is the array which holds the flags for all the primes upto √(2³¹-1), i.e. the square-root of the max limit, and all the primes are stored in the 'primes' array. Later, these primes are used to determine whether a number is a composite or not within a certain range in the segmented sieve. To avoid overflow and sign bit problems, unsigned type is used.

A little explanation:

First of what what these macros mean?
#define MAX 46656
#define LMT 216
#define LEN 4830
#define RNG 100032

MAX is the sqrt of maximum possible input, in case of here, the maximum is integer range sqrt of which is almost MAX used here. So, MAX is not maximum allowed input, it is just sqrt of maximum input which is pretty big as 2147483647 i.e. 32 bit signed integer maximum.
LMT is sqrt of MAX. We all know, we run sieve upto sqrt MAX
LEN is the maximum possible different primes that can be stored using this algorithm with specific range defined as RNG, on which the segmented sieve will run and collect the primes out of it.

Now the next two vital macros:
#define chkC(x,n) (x[n>>6]&(1<<((n>>1)&31)))
#define setC(x,n) (x[n>>6]|=(1<<((n>>1)&31)))
And why we divide by 64:

Ok, yes, it is clearly bit shifting. But you must know what we do in bitwise sieve first in order to get this. Instead of using a whole array position to store just one flag, we can use its each 32 bits to store one flag, which saves memory by a factor 1/32. So its very logical to capture memory upto MAX/32, but why MAX/64 and RNG/64 here?
Because, we really have no point of handling the even number as 2 is the only even prime and we can handle it manually, without any stress. So, if we do not consider the even numbers at all, the total numbers are again reduced by a factor 1/2, isn't it? So what we get total is MAX/32/2 = MAX/64, same for RNG.

Now, the two macros chkC and setC is pretty straight forward. chkC checks if a specific bitflag is 1 or 0, and setC sets a specific bitflag 1 to mark it as a composite. They work similarly, so I will explain only the chkC part.

In bitwise sieve, where is a specific value n located? Obviously (n/32)^th index, and on that index, (n%32)^th bit from LSB (right hand side). But we just said before, we are interested with only odd numbers, so we map n with n/2 as follows:

Actual numbers
 1   2   3   4   5   6   7   8   9 ...........   n     ;[n is odd]
 |   |   |   |   |   |   |   |   | ...........   |
 0   x   1   x   2   x   3   x   4 ........... (n/2)
Position on which they are represented in the bitstrings.

So, n is actually n/2, which implies the previous statement: n's (actually n/2 's) position is in index [n/2/32] = [n/64] = [n>>6] and on the bit position (n/2)%32 = (n>>1)&31 ;[ We know, modding with a power of 2 is same as ANDing with (same power of 2)-1 ]. The rest is, how we check / set this specific bit. I have another post explaining these operations: Bitwise operations in C: Part 3, and obviously you can google it :)

Calculate nCr using dp

Calculate ⁿC_r with out having overflow when it is guaranteed that the final result will not overflow:

From pascal's triangular relation, we get,
ⁿC_r = ^n-1C_r + ^n-1C_r-1

Using this recursive formula directly will lead the program to exceed the time limit, as this may calculate the same value for many times which is un-necessary and we can remove this part by saving the states which means by using dynamic programming concepts.

In this formulation, one thing is to be noted that n and r keep decreasing, and sometimes is is possible that n becomes smaller than r. So considering these cases we get our base conditions for the recursive formula.

We know,
ⁿC_n = 1
ⁿC₁ = n
ⁿC₀ = 1
and
ⁿC_r = ^n-1C_r + ^n-1C_r-1

So, we can build the recursive function as follows:

function nCr(n, r):
    if n == r:
        return 1
    if r == 1:
        return n
    if r == 0:
        return 1
    return nCr(n-1, r) + nCr(n-1, r-1)

Now, to reduce recursive steps, we maintain a table for saving the values of ⁿC_r of intermediate steps. So, when we face a sub-problem which is already solved, we can look up its value from the pre-calculation table.

table dp[N][R]

function nCr(n, r):
    if n == r:
        dp[n][r] = 1
    if r == 1:
        dp[n][r] = n
    if r == 0:
        dp[n][r] = 1
    if dp[n][r] is not yet calculated:
        dp[n][r] = nCr(n-1,r) + nCr(n-1,r-1)
    return dp[n][r]

Here is a sample code written in C++ which demonstrates the idea. (It is assumed that MAX N is 65 and N >= R).

#include <stdio.h>

#define i64 unsigned long long

i64 dp[66][33];

i64 nCr(int n, int r)
{
    if(n==r) return dp[n][r] = 1;
    if(r==0) return dp[n][r] = 1;
    if(r==1) return dp[n][r] = (i64)n;
    if(dp[n][r]) return dp[n][r];
    return dp[n][r] = nCr(n-1,r) + nCr(n-1,r-1);
}

int main()
{
    int n, r;
    while(scanf("%d %d",&n,&r)==2)
    {
        r = (r<n-r)? r : n-r;
        printf("%llu\n",nCr(n,r));
    }
    return 0;
}

Plain and simple!!!

Extended Euclidean Algorithm

Extended Euclidean Algorithm is an extension of standard Euclidean Algorithm for finding the GCD of two integers a and b. It also calculates the values of two more integers x and y such that: ax + by = gcd(a,b); where typically either x or y is negative. This algorithm is generally used to find multiplicative inverse in a finite field, because, if ax + by = gcd(a,b) = 1, i.e. a and be are co-primes, then x is the modular multiplicative inverse of a modulo b, and similarly, y is the modular multiplicative inverse of b modulo a.

This method computes expressions of the form r_i = ax_i + by_i for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:

By substitution, this gives:

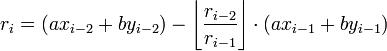
The first two values are the initial arguments to the algorithm:

r₁ = a = a(1) + b(0)

r₂ = b = a(0) + b(1)

The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.

Example: Compute the GCD of 120 and 23. Or, more formally, compute: x, y, g for 120x + 23y = g; where x, y are two integers and g is the gcd of 120 and 23...

The computation proceeds as follows:

Initial values:
Step 1: Reminder = 120;
Combine terms: 120 = 120 x 1 + 23 x 0

Step 2: Reminder = 23;
Combine terms: 23 = 120 x 0 + 23 x 1

Iterative steps:
Step 3: Quotient = 120 / 23 = 5; Reminder = 120 % 23 = 5;
5 = 120 - 23 x 5
=> 5 = (120 x 1 + 23 x 0) - (120 x 0 + 23 x 1) x 5 ;[from Step 1 and 2]
=> 5 = 120 x 1 + 23 x -5

Step 4: Quotient = 23 / 5 = 4; Reminder = 23 % 5 = 3;
3 = 23 - 5 x 4
=> 3 = (120 x 0 + 23 x 1) - (120 x 1 + 23 x -5) x 4 ;[from Step 2 and 3]
=> 3 = 120 x -4 + 23 x 21

Step 5: Quotient = 5 / 3 = 1; Reminder = 5 % 3 = 2;
2 = 5 - 3 x 1
=> 2 = (120 x 1 + 23 x -5) - (120 x -4 + 23 x 21) x 1 ;[from Step 3 and 4]
=> 2 = 120 x 5 + 23 x -26

Step 6: Quotient = 3 / 2 = 1; Reminder = 3 % 2 = 1;
1 = 3 - 2 x 1
=> 1 = (120 x -4 + 23 x 21) - (120 x 5 + 23 x -26) x 1 ;[from Step 4 and 5]
=> 1 = 120 x -9 + 23 x 47
End of Algorithm.

The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47, and obviously g = gcd(120,23) = 1

This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.

−9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.

Algorithm:
By routine algebra of expanding and grouping like terms (refer to the previous example), the following algorithm for iterative method is obtained:

1. Apply Euclidean algorithm, and let q_n(n starts from 1) be a finite list of quotients in the division.
2. Initialize x₀, x₁ as 1, 0, and y₀, y₁ as 0,1 respectively.
3. Then for each i so long as q_i is defined,
• Compute x_i+1= x_i-1- q_ix_i
• Compute y_i+1= y_i-1- q_iy_i
• Repeat the above after incrementing i by 1.
4. The answers are the second-to-last of x_n and y_n.

Sample Program:
Here is a sample program written in C++ which implements the Extended Euclidean Algorithm:

#include <stdio.h>
/*
Takes a, b as input.
Returns gcd(a, b).
Updates x, y via pointer reference.
*/
int Extended_Euclid(int A, int B, int *X, int *Y)
{
    int x, y, u, v, m, n, a, b, q, r;
 
    /* B = A(0) + B(1) */
    x = 0; y = 1;
 
    /* A = A(1) + B(0) */
    u = 1; v = 0;
 
    for (a = A, b = B; 0 != a; b = a, a = r, x = u, y = v, u = m, v = n)
    {
        /* b = aq + r and 0 <= r < a */
        q = b / a;
        r = b % a;
 
        /* r = Ax + By - aq = Ax + By - (Au + Bv)q = A(x - uq) + B(y - vq) */
        m = x - (u * q);
        n = y - (v * q); 
    }   
 
    /* Ax + By = gcd(A, B) */
    *X = x; *Y = y;
 
    return b;
}

int main()
{
    int a, b, x, y, g;
    scanf("%d %d", &a, &b);
    g = Extended_Euclid(a, b, &x, &y);
    printf("X = %d; Y = %d; G = %d\n", x, y, g);
    return 0;
}

Python implementation:

def Extended_Euclid(a, b):
    x, last_x = 0, 1
    y, last_y = 1, 0
 
    while b:
        quotient = a / b
        a, b = b, a % b
        x, last_x = last_x - quotient*x, x
        y, last_y = last_y - quotient*y, y
 
    return (last_x, last_y, a)

For complete reading, click here. It is also useful to have a look at the Chinese Remainder Theorem.

Hope this will help...

Largest impossible score

Problem:
If two possible points in a game is p and q, what is the largest impossible score of the game which can't be achieved? Or it can't be determined? In other words, for integers p, q ≥ 0, what is the maximum number m which can't be written as a linear combination of p, q, i.e. px + qy, where, x, y ≥ 0.

Solution:
The score can only be determined when p and q are co-primes, i.e. g = GCD(a,b) = 1. Otherwise, we can only make the multiples of g and the remaining numbers can't be made which means the maximum number can't be determined, or infinite! This also covers the case if exactly one of p or q is 0.

One other required condition is p,q > 1. If anyone of p or q is 1, there is no such score which can't be achieved, i.e. answer will be 0. If p and q both are 0, we can't even make any score...

Now, we can arrange the numbers from 0 to p*q-1 in a rectangular array as follows:

   0         1        .......       q-1
   q        q+1       .......       2q-1
  ...       ...       .......       ...
  ...       ...       .......       ...
(p-1)q   (p-1)(q-1)   .......       pq-1

For example, if p = 3 and q = 7, we have the following table:

(0)    1     2   (3)   4     5   (6)
 7     8    (9)   10   11   (12)  13
 14   (15)   16   17  (18)   19   20

We have circled the multiples of p in the above table and claim these observations:

• There will be q circled numbers. As we have exactly p numbers in each of q columns, so each column will have exactly one circled number, i.e. multiple of p, which implies, there will be a total of q circled number in this table.


• No two circled numbers are in same same column and there will be only one circled number in any column. For the same reason stated above, exactly one circled number in each column.


• Any circled number is possible. This is trivial, because, the circled numbers are multiple of one of the two given numbers, i.e. in the form p*x + q*0 or p*0 + q*x.


• Any number below the circled one in the same column is possible. We have seen any circled number is possible. A circled number is the first multiple of p in the respective column, i.e. n*p, where n ≥1, so the following numbers in the column will be: n*p + q, n*p + 2*q. n*p + 3*q, ... ... ... which are always possible.


• Any number above the circled one in the same column is impossible. This is also explained in the previous step. As any circled number in a column is the first one which is a multiple of one element, the number above this one will be neither the multiple of any of the two numbers. So it is impossible.


• Any number ≥ p*q is possible. As we complete p rows of the table with q columns, we already have one circled number in each column, so, any number > p*q-1 (i.e. the last element of the table) will be surely following any of the q circled numbers, so any number starting from the p+1^th row, starting from p*q will be possible.

Now considering all these observations, we can see that, largest impossible number is the number just above the last circled number. The last circled number is p*q-p, i.e. 21-3 = 18 and number above it is (p*q-p)-q, i.e. 18-7 = 11. So in general, largest impossible number is: p*q - p - q.

Conclusion:
If you are given p, q :: two positive numbers, the largest number, m, which can't be expressed as a linear combination of p, q i.e. in the form px + qy, where x and y are two non-negative numbers, is p * q - p - q, when p, q > 1 and GCD(p, q) is 1 i.e. p, q are co-primes.

Binary GCD algorithm

Here is a sample code for calculating GCD bitwise:

typedef unsigned int ui;

ui gcd(ui u, ui v)
{
    ui shift, diff;
    
    if (u == 0 || v == 0)
        return u | v;
    
    /* Let shift := lg K,
    where K is the greatest power of 2 dividing both u and v. */

    for (shift = 0; ((u | v) & 1) == 0; ++shift)
    {
        u >>= 1;
        v >>= 1;
    }
    
    while ((u & 1) == 0)
        u >>= 1;
        
    /* From here on, u is always odd. */

    do {
        while ((v & 1) == 0)
            v >>= 1;
            
        /* Now u and v are both odd, so diff(u, v) is even.
        Let u = min(u, v), v = diff(u, v)/2. */

        if (u < v)
            v -= u;
        else
        {
            diff = u - v;
            u = v;
            v = diff;
        }
        v >>= 1;
    
    } while (v != 0);
    
    return u << shift;
}

Actually, this algorithm outperforms the basic euclidean algorithm, so their asymptotic performance are same. According to Wikipedia, it is sometimes 60% faster than normal euclidean algorithm [proven].

But who needs it when he can do the following:

int gcd(int a, int b)
{
    while(b) b ^= a ^= b ^= a %= b;
    return a;
}

Stunned? oh that's normal...

Craziest Language Ever !!!

Just have a look at these programming languages... They are really crazy as their names.

1. Brainf**k
2. Intercal
3. Whitespace

These are called esoteric programming languages.

Factorial of negative number

Is it possible to find factorial of negative numbers?

By definition,
N! = 1 x 2 x .... x N
⇒ N! = 1 x 2 x .... x N x (N+1) / (N+1)
⇒ N! = (N+1)! / (N+!)

Now, let's try some values:
3! = 4! / 4 = 6
2! = 3! / 3 = 2
1! = 2! / 2 = 1
0! = 1! / 1 = 1

So, that's how 0! = 1. Let's not stop at 0!, if we continue this fashion, we get:
(-1)! = 0! / 0 = Undetermined

Many people still keeps arguing about whether x / 0 = +∞ or Undefined, it really doesn't matter though, because it is well established that anything divided by zero is undefined.

However, in this post, we are going to talk about a problem from UVa Online Judge, UVa-10323 (Factorial! You Must be Kidding!!!). This problem actually requires you to calculate even the factorials of negative numbers, which does not really exist in real world.

In this context, we are forced to assume that x / 0 = +∞. There was a mistake on my previous post, this section is updated as per the comment from a fellow reader আহনাফ তাহমিদ:
(-1)! = 0! / 0 = +∞
(-2)! = (-1)! / -1 = -∞
(-3)! = (-2)! / -2 = +∞
(-4)! = (-3)! / -3 = -∞
(-5)! = (-4)! / -4 = +∞
and so on..

Hence, we can see that, if N is odd, then (-N)! = +∞, otherwise (-N)! = -∞. Note that, this specific problem statement calls +∞ as Overflow and -∞ as Underflow.

Hope it helps!

Easy problems at UVA OJ

Here are some suggestion about some very easy problems on UVA Online Judge

Programming is fun!!! especially for the beginners, and new programmers find a great inspiration on solving easy problems first as these problems are good for learning the ropes. To help some of my new friends i.e. new programmer friends who intend to solve problems on UVA OJ, here is a list of very easy problems.

Some problems among these may not seem so easy at a first glance, but after a little thinking, they will be easily solved. These problems will also help you to understand common programming techniques along with the verdict variations.


136 very easy problems for beginners:

   105    119    136    138    145    154    190    200
   256    264    272    278    294    332    344    355
   362    374    378    382    389    394    401    409
   412    412    414    417    422    424    426    438
   441    444    445    455    458    460    465    466
   468    474    476    477    478    482    483    484
   486    489    490    492    494    495    496    498
   499    530    535    543    568    573    575    579
   583    587    591    621    713    834    900    944
   974  10006  10008  10013  10018  10019  10035  10055
 10060  10071  10078  10079  10093  10104  10110  10161
 10195  10209  10221  10242  10281  10297  10302  10323
 10340  10347  10407  10432  10451  10469  10490  10499
 10515  10522  10533  10573  10591  10678  10679  10683
 10783  10784  10790  10812  10815  10922  10929  10931
 10991  11058  11121  11152  11172  11192  11192  11219
 11220  11233  11332  11343  11388  11417  11437  11455

Good Luck !!!

Negative Base Number System

Negative-base systems can accommodate all the same numbers as standard place-value systems; but both positive and negative numbers are represented without the use of a minus sign (or, in computer representation, a sign bit); this advantage is countered by an increased complexity of arithmetic operations. The need to store the "information" normally contained by a negative sign often results in a negative-base number being one digit longer than its positive-base equivalent.


The common names for negative-base positional numeral systems are formed by prefixing nega- to the name of the corresponding positive-base system; for example, negadecimal (base -10) corresponds to decimal (base 10), negaternary (base -3) to ternary (base 3), and negabinary (base -2) to binary (base 2).

Denoting the base as − r, every integer a can be written uniquely as:

where each digit d_k is an integer from 0 to r − 1 and the leading digit d_n is > 0 (unless n=0). The base − r expansion of a is then given by the string d_nd_n-1.....d₁d₀.


Calculation:

The base − r expansion of a number can be found by repeated division by − r, recording the non-negative remainders of 0,1,2,.........,r-1; and concatenating those remainders, starting with the last. Note that if a / b = c, remainder d, then bc + d = a. For example, 146 in negaternary:

146 / -3 = -48; reminder = 2
-48 / -3 =  16; reminder = 0
 16 / -3 =  -5; reminder = 1
 -5 / -3 =   2; reminder = 1
  2 / -3 =   0; reminder = 2

Therefore, the negaternary expansion of 146 is 21102.

Note that in most programming languages, the result (in integer arithmetic) of dividing a negative number by a negative number is rounded towards 0, usually leaving a negative remainder; to get the correct result in such case, computer implementations of the above algorithm should add 1 and r to the quotient and remainder respectively.

The numbers -15 to 15 with their expansions in a number of positive and corresponding negative bases are:

Decimal	Negadecimal	Binary	Negabinary	Ternary	Negaternary
-15	25	-1111	110001	-120	1220
-14	26	-1110	110110	-112	1221
-13	27	-1101	110111	-111	1222
-12	28	-1100	110100	-110	1210
-11	29	-1011	110101	-102	1211
-10	10	-1010	1010	-101	1212
-9	11	-1001	1011	-100	1200
-8	12	-1000	1000	-22	1201
-7	13	-111	1001	-21	1202
-6	14	-110	1110	-20	20
-5	15	-101	1111	-12	21
-4	16	-100	1100	-11	22
-3	17	-11	1101	-10	10
-2	18	-10	10	-2	11
-1	19	-1	11	-1	12
0	0	0	0	0	0
1	1	1	1	1	1
2	2	10	110	2	2
3	3	11	111	10	120
4	4	100	100	11	121
5	5	101	101	12	122
6	6	110	11010	20	110
7	7	111	11011	21	111
8	8	1000	11000	22	112
9	9	1001	11001	100	100
10	190	1010	11110	101	101
11	191	1011	11111	102	102
12	192	1100	11100	110	220
13	193	1101	11101	111	221
14	194	1110	10010	112	222
15	195	1111	10011	120	210

Note that the base − r expansions of negative integers have an even number of digits, while the base − r expansions of the non-negative integers have an odd number of digits.

Program for calculating Negabinary

In python:

def negabinary(i):
    digits = []  
    while i != 0:
        i, remainder = divmod(i, -2)
        if remainder < 0:
            i, remainder = i + 1, remainder + 2
        digits.insert(0, str(remainder))
    return ''.join(digits)

In C++:

string negabinary(int i)
{
    int reminder;
    string digits;
    while(i != 0)
    {
        reminder = i % -2;
        i /= -2;
        if(reminder < 0)
        {
            i++;
            reminder += 2;
        }
        digits.push_back(reminder+'0');
    }
    reverse(digits.begin(),digits.end());
    return digits;
}

The same procedure it to be followed for calculating other negative number system.

Source: Wikipedia