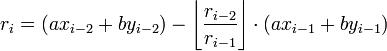This method computes expressions of the form ri = axi + byi for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:
By substitution, this gives:
The first two values are the initial arguments to the algorithm:
- r1 = a = a(1) + b(0)
- r2 = b = a(0) + b(1)
The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.
Example: Compute the GCD of 120 and 23. Or, more formally, compute: x, y, g for 120x + 23y = g; where x, y are two integers and g is the gcd of 120 and 23...
The computation proceeds as follows:- Initial values:
Step 1: Reminder = 120;
Combine terms: 120 = 120 x 1 + 23 x 0
Step 2: Reminder = 23;
Combine terms: 23 = 120 x 0 + 23 x 1
Iterative steps:
Step 3: Quotient = 120 / 23 = 5; Reminder = 120 % 23 = 5;
5 = 120 - 23 x 5
=> 5 = (120 x 1 + 23 x 0) - (120 x 0 + 23 x 1) x 5 ;[from Step 1 and 2]
=> 5 = 120 x 1 + 23 x -5
Step 4: Quotient = 23 / 5 = 4; Reminder = 23 % 5 = 3;
3 = 23 - 5 x 4
=> 3 = (120 x 0 + 23 x 1) - (120 x 1 + 23 x -5) x 4 ;[from Step 2 and 3]
=> 3 = 120 x -4 + 23 x 21
Step 5: Quotient = 5 / 3 = 1; Reminder = 5 % 3 = 2;
2 = 5 - 3 x 1
=> 2 = (120 x 1 + 23 x -5) - (120 x -4 + 23 x 21) x 1 ;[from Step 3 and 4]
=> 2 = 120 x 5 + 23 x -26
Step 6: Quotient = 3 / 2 = 1; Reminder = 3 % 2 = 1;
1 = 3 - 2 x 1
=> 1 = (120 x -4 + 23 x 21) - (120 x 5 + 23 x -26) x 1 ;[from Step 4 and 5]
=> 1 = 120 x -9 + 23 x 47
End of Algorithm.
The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47, and obviously g = gcd(120,23) = 1
This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.
- −9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.
By routine algebra of expanding and grouping like terms (refer to the previous example), the following algorithm for iterative method is obtained:
- Apply Euclidean algorithm, and let qn(n starts from 1) be a finite list of quotients in the division.
- Initialize x0, x1 as 1, 0, and y0, y1 as 0,1 respectively.
- Then for each i so long as qi is defined,
- Compute xi+1= xi-1- qixi
- Compute yi+1= yi-1- qiyi
- Repeat the above after incrementing i by 1.
- The answers are the second-to-last of xn and yn.
Here is a sample program written in C++ which implements the Extended Euclidean Algorithm:
#include <stdio.h>
/*
Takes a, b as input.
Returns gcd(a, b).
Updates x, y via pointer reference.
*/
int Extended_Euclid(int A, int B, int *X, int *Y)
{
int x, y, u, v, m, n, a, b, q, r;
/* B = A(0) + B(1) */
x = 0; y = 1;
/* A = A(1) + B(0) */
u = 1; v = 0;
for (a = A, b = B; 0 != a; b = a, a = r, x = u, y = v, u = m, v = n)
{
/* b = aq + r and 0 <= r < a */
q = b / a;
r = b % a;
/* r = Ax + By - aq = Ax + By - (Au + Bv)q = A(x - uq) + B(y - vq) */
m = x - (u * q);
n = y - (v * q);
}
/* Ax + By = gcd(A, B) */
*X = x; *Y = y;
return b;
}
int main()
{
int a, b, x, y, g;
scanf("%d %d", &a, &b);
g = Extended_Euclid(a, b, &x, &y);
printf("X = %d; Y = %d; G = %d\n", x, y, g);
return 0;
}
Python implementation:
def Extended_Euclid(a, b):
x, last_x = 0, 1
y, last_y = 1, 0
while b:
quotient = a / b
a, b = b, a % b
x, last_x = last_x - quotient*x, x
y, last_y = last_y - quotient*y, y
return (last_x, last_y, a)
For complete reading, click here. It is also useful to have a look at the Chinese Remainder Theorem.
Hope this will help...